
Daisy’s
Theorem
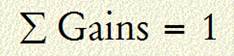
Electronics
describes circuits in terms of voltage and current. An alternative view
is to describe the circuit in terms of inputs, outputs, and input to output
gains. For a linear circuit, the voltage at a circuit node is the product
of input voltage and gain. Additional inputs create additional terms in
the node equation. The circuit adds these terms and is viewed as a
summing circuit.
Daisy’s Theorem states that the sum of ALL
voltage gains is equal to one. The key word is ALL. The theorem applies to each
node in the circuit. Different nodes may have different gains, but for
each node the sum of the gains is equal to one. This also
true for the entire circuit.
The voltage at a circuit node contains
signals that you want plus components that you don’t want. If we describe
the circuit in terms of gains, the circuit will have signal gains and noise
gains. The signal gains come from circuit inputs. The noise gains
can come from other sources such as ground or the power supply.
Daisy’s theorem applies to linear
systems. It is independent of circuit implementation. A
mathematical description is presented on the Technical
Daisy page.
Interpretation
Gain is normally associated with active
circuits and a gain value greater than one is implied. Loss (gain less
than one) is associated with passive circuits. Active circuits have gain,
Passive circuits have loss. Daisy’s theorem states that if you add the
gains, Active circuits have the same amount of total gain as passive
circuits. Both have no total gain. This requires quite a bit of
digesting.
Another interpretation is that for an op-amp
circuit, the positive gain is one more than the negative gain. Consider a
non-inverting amplifier. In the Legacy 1 + RF/RI formula, RF/RI is the
negative gain. You need negative gain to get positive gain. If you
disconnect RI, the negative gain is zero and the positive gain is one.
A gain sum of one must be present for all
frequencies. At a frequency above the circuit bandwidth, some other gain
needs to compensate for the loss of signal gain. If the circuit is AC
coupled, some other gain must compensate for the loss of signal gain at
DC. This also requires a bit of digesting.
Applications
K9 Design uses Daisy’s Theorem to determine the ground gain
needed for a new design. There are many other applications. Consider the
following:
Bandwidth
For Op-amp circuits, the product of the gain and bandwidth is often a constant. The gain is the positive circuit gain, sometimes called the Noise gain. Daisy’s Theorem provides an easy way to get the Noise Gain for inverting circuits. Just add 1 to the magnitude of the negative gain.
Audio Amplifier Noise Reduction
You have been asked to design an amplifier to boost an audio signal by a factor of two. The design should minimize the amount of ground noise added to the output. You can design a non-inverting amplifier with a gain of +2 or an inverting amplifier with a gain of minus 2. Which design should you choose?
Daisy’s Theorem has the answer. The gain from
the ground node is equal to 1 minus the signal gain. The non-inverting
amplifier will have a ground gain of minus 1. The inverting amplifier has a
ground gain of +3. The non-inverting amplifier will add 10db less ground noise
to the output.
You can extend the above to any gain. The conclusion will be the same:
Use Non-Inverting Amplifiers to reduce ground noise.
A detailed discussion is on the Noise Reduction Example page.
Note that reducing ground noise is not always
a good idea. For example, if the amplifier is part of a Digital system which
has quantizing noise
and ground noise with a White
noise spectrum, you may want ground noise to improve the perceived audio
quality.
Note also that Ground Noise is only one of
many audio amplifier design considerations. We have not considered amplifier
distortion nor other imperfections. The topic is very
complicated. We need some smart dogs.
Op-Amp Amplifier Power Supply Noise Rejection
Op-amp circuits have a finite bandwidth. The power supply noise rejection tends to become worse for frequencies above the bandwidth. Is there a correlation between circuit bandwidth and power supply noise rejection?
Answer: Yes. The decrease in circuit gain is
compensated by an increase in the gain from the power supply leads. A detailed
analysis is presented on the Technical page.
Summary
Daisy’s Theorem states that the sum of the
circuit gains is equal to one. Knowledge of the circuit is not required.
Daisy is no longer with us. This theorem is dedicated to Daisy. To honor her, I ask that you keep the name.
There are many other applications of Daisy’s Theorem. If you find a novel application or have a question, I can be reached at k9analysis@netzero.net.