Ladder Output Impedance

There was a miscommunication. The output impedance, not the input impedance, is required. Even though this rarely happens, K9 Analysis can provide a solution.

The approach in this case is a little different. We will add an input to derive an equation for the output impedance. A current source, I, connected to the output will allow the output impedance to be calculated via the transfer function from I to Vout.

Zout = Vout / I

Think of I as a test current. When you want to find a node impedance, connect a 1 amp current source and see how much voltage is developed. Don’t try this on a real circuit. It only works for linear circuit analysis and AC simulations. Let the fireworks begin.

The general schematic with the current source is shown below.

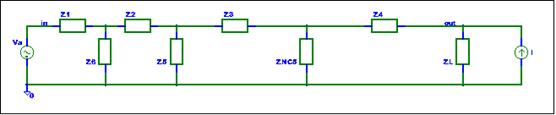
The gain from a current source to a summing node is the parallel impedance of the node. If the current flow into the node the gain is positive; if it flows out of the node the gain is negative. The modified SFG is shown below.

Analyze the SFG

The I node did not add any loops to the SFG. From the Ladder analysis

L1 = ZP2/Z2 * ZP1/Z2

L2 = ZP3/Z3 * ZP2/Z3

L3 = ZPout/Z4 * ZP3/Z4

L1 and L3 are non-touching loops.

The determinant is:

D = 1 + (L1 + L2 + L3) + (L1 * L3)

When calculating the gain from I to Vout, we will use Superposition and set Va equal to zero.

There is one path from I to Zout. This path touches only L3. The associated delta for this path is:

D3 = 1 + (L1 + L2)

The transfer function is.

Zout = Vout / I = (ZPout* D3)/D

Check the Answer

If Z4 is opened, the output impedance should be equal to Zl.

With Z4 infinite, ZPout will be equal to Zl and L3 will be equal to zero. With L3 equal to zero, D3 will be equal to D. Zout is hence equal to ZL if Z4 is equal to zero.

Conclusion

This example illustrated how to add a test current to allow the equation for a node impedance to be derived.

Adding a test current is an easy way to measure the impedance of a node. A current source has high impedance and will not alter linear circuit operation. No loops are added to the SFG. You can use this trick in an AC simulation. It is difficult to implement on a real circuit.

ZPout is the output impedance if there are no circuit interactions. The ∆ terms provide the corrections. ∆ compensates for the entire circuit. ∆3 is needed to cancel the compensation for the non-touching loops.

Summary

You can use the test current trick on any node. The K9 node impedance may need a correction for circuit interactions (loops).

You can extend the analysis to larger latter networks. Note that only the ∆ terms change.

You can expand on the concepts described in this ladder example to find general circuit equations. The idea behind K9 is not to analyze a single specific circuit. It is actually easier to derive the gain equation for a class of circuits. Who said that analog circuits are difficult?

The telephony guys may want an equation for the two wire insertion loss of the ladder circuit. Reader exercise.

In the next example we will derive the general gain equation for many single op-amp circuits.